月別: 2019年12月

KLDivergenceとJSDivergence

投稿者: utsubo 投稿日: in python

Pythonのコード作成したのでメモ

KLダイバージェンス

$$D_{KL}(P||Q) = \sum_x p(x) \, \log \frac{P(x)}{Q(x)}$$

JSダイバージェンス

$$D_{JS}(P||Q)=\frac{1}{2}\bigg\{ D_{KL}(P \, || \, R)+D_{KL}(Q \, || \, R) \bigg\}$$
$$R = \frac{P + Q}{2}$$

プログラム

ここを参考に

データ

まずはデータの準備


import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

np.random.seed(12345)
a=np.random.normal(40,10, size=200)
b=np.random.normal(70,15, size=100)
c=np.random.normal(30,2, size=70)
d=np.random.normal(150,10, size=150)

plt.figure()
plt.hist(a,alpha=0.3,bins=20,histtype="stepfilled",color="r",label="a")
plt.hist(b,alpha=0.3,bins=20,histtype="stepfilled",color="b",label="b")
plt.hist(c,alpha=0.3,bins=20,histtype="stepfilled",color="black",label="c")
plt.hist(d,alpha=0.3,bins=20,histtype="stepfilled",color="y",label="d")
plt.legend()
plt.show()

ヒストグラム

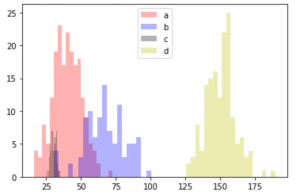
KLダイバージェンス


def KLDivergence(a, b, bins=20, epsilon=.00001):
    min_value=min(min(a),min(b))
    max_value=max(max(a),max(b))
    # サンプルをヒストグラムに, 共に同じ数のビンで区切る
    a_hist, _ = np.histogram(a, range=(min_value,max_value),bins=bins) 
    b_hist, _ = np.histogram(b, range=(min_value,max_value),bins=bins)
    
    # 合計を1にするために全合計で割る
    a_hist = (a_hist+epsilon)/np.sum(a_hist)
    b_hist = (b_hist+epsilon)/np.sum(b_hist)
    
    # 本来なら a の分布に0が含まれているなら0, bの分布に0が含まれているなら inf にする
    return np.sum([ai * np.log(ai / bi) for ai, bi in zip(a_hist, b_hist)])

JSダイバージェンス


def JSDivergence(a, b, bins=20, epsilon=.00001):
    min_value=min(min(a),min(b))
    max_value=max(max(a),max(b))
    # サンプルをヒストグラムに, 共に同じ数のビンで区切る
    a_hist, _ = np.histogram(a, range=(min_value,max_value),bins=bins) 
    b_hist, _ = np.histogram(b, range=(min_value,max_value),bins=bins)

    # 合計を1にするために全合計で割る
    a_hist = (a_hist+epsilon)/np.sum(a_hist)
    b_hist = (b_hist+epsilon)/np.sum(b_hist)
    
    r_hist = (a_hist + b_hist)/2.0
    
    ar= np.sum([ai * np.log(ai / ri) for ai, ri in zip(a_hist, r_hist)])
    br= np.sum([bi * np.log(bi / ri) for bi, ri in zip(b_hist, r_hist)])
    return (ar+br)/2.0

実験

まずはaとbの分布を調べます。


kl1=KLDivergence(a,b)
js1=JSDivergence(a,b)

kl2=KLDivergence(b,a)
js2=JSDivergence(b,a)
print("kl1=",kl1,",kl2=",kl2)
print("js1=",js1,",js2=",js2)


kl1= 4.804620164702722 ,kl2= 8.66117091460137
js1= 0.44568757334874426 ,js2= 0.44568757334874426

KLダイバージェンスはaとbを入れ替えると値が変わりますが、JSダイバージェンスでは同じです。

つぎに、分布間でのKLダイバージェンスとJSダイバージェンスの値を調べます


# 一致　
kl1=KLDivergence(a,a)
kl2=KLDivergence(a,a)
js=JSDivergence(a,a)
print("一致:kl1=",kl1,",kl2=",kl2,",js=",js)

# 含まれる
kl1=KLDivergence(a,c)
kl2=KLDivergence(c,a)
js=JSDivergence(a,c)
print("含有:kl1=",kl1,",kl2=",kl2,",js=",js)

# 重なる
kl1=KLDivergence(a,b)
kl2=KLDivergence(b,a)
js=JSDivergence(a,b)
print("重複:kl1=",kl1,",kl2=",kl2,",js=",js)

# 小別離
kl1=KLDivergence(b,d)
kl2=KLDivergence(d,b)
js=JSDivergence(b,d)
print("小離:kl1=",kl1,",kl2=",kl2,",js=",js)

# 大別離
kl1=KLDivergence(a,d)
kl2=KLDivergence(d,a)
js=JSDivergence(a,d)
print("大離:kl1=",kl1,",kl2=",kl2,",js=",js)


一致:kl1= 0.0 ,kl2= 0.0 ,js= 0.0
含有:kl1= 8.982185089568121 ,kl2= 1.5818474236167488 ,js= 0.3961382475750016
重複:kl1= 4.804620164702722 ,kl2= 8.66117091460137 ,js= 0.44568757334874426
小離:kl1= 14.585645733703917 ,kl2= 14.484008742932685 ,js= 0.6931379306807828
大離:kl1= 14.9325435215302 ,kl2= 15.170878470071264 ,js= 0.6931412821202988

結果を見ると、距離の遠い順にKLダイバージェンス、JSダイバージェンスの値が大きくなっています。KLダイバージェンスの場合には、どちらを基準にするかによって変わってくるので注意が必要みたいですね。