このあたりを参考に書き直してみました。
プログラム
import chainer
import chainer.links as L
import chainer.functions as F
import numpy as np
from chainer import optimizers
from chainer.datasets import tuple_dataset
from chainer import reporter
import matplotlib.pyplot as plt
class MyClassifier(chainer.Chain):
def __init__(self, seqlen, out_units=1, dropout=0.1):
super(MyClassifier, self).__init__()
with self.init_scope():
self.encoder = L.LSTM(seqlen, out_units)
self.dropout = dropout
def forward(self, xs, ys):
concat_outputs =F.concat( self.predict(xs), axis=0)
concat_truths = F.concat(ys, axis=0)
loss = F.mean_squared_error(concat_outputs, concat_truths)
reporter.report({'loss': loss}, self)
return loss
def predict(self, xs, softmax=False, argmax=False):
concat_encodings = F.dropout(self.encoder(xs), ratio=self.dropout)
if softmax:
return F.softmax(concat_encodings).array
elif argmax:
return self.xp.argmax(concat_encodings.array, axis=1)
else:
return concat_encodings
def reset_state(self):
self.encoder.reset_state()
# main
if __name__ == "__main__":
# データ
def get_dataset(N,st=0,ed=2*np.pi):
xval = np.linspace(st,ed, N) # x軸の値
y = np.sin(xval) # y軸の値
return y,xval
# 0-2piまでを100等分
N = 100
train_ds,train_xval = get_dataset(N)
# valid
N_valid = 50
valid_ds,valid_xval = get_dataset(N_valid,2*np.pi,3*np.pi)
# 学習パラメータ
batchsize = 10
n_epoch = 1000
seqlen=10
gpu = -1
def seq_split(seqlen,ds,xval):
X=[] # seqlen 分Y軸の値を取り出し
y=[] # seqlen+1のY軸の値を正解として格納
ret_xval=[] # その時のX軸の値
for i in range(len(ds)-seqlen-1):
X.append(np.array(ds[i:i+seqlen]))
y.append(np.array([ds[i+seqlen]]))
ret_xval.append(xval[i+seqlen])
return X,y,ret_xval
X_train,y_train,_=seq_split(seqlen,train_ds,train_xval)
train=tuple_dataset.TupleDataset(np.array(X_train, dtype=np.float32), np.array(y_train, dtype=np.float32))
X_valid,y_valid,_=seq_split(seqlen,valid_ds,valid_xval)
valid=tuple_dataset.TupleDataset(np.array(X_valid, dtype=np.float32), np.array(y_valid, dtype=np.float32))
# モデル作成
model = MyClassifier(seqlen=seqlen)
optimizer = optimizers.Adam()
optimizer.setup(model)
train_iter = chainer.iterators.SerialIterator(train, batchsize)
valid_iter = chainer.iterators.SerialIterator(valid, batchsize, repeat=False, shuffle=False)
updater = chainer.training.updaters.StandardUpdater(train_iter, optimizer, device=gpu)
trainer = chainer.training.Trainer(updater, (n_epoch, 'epoch'), out="snapshot")
trainer.extend(chainer.training.extensions.Evaluator(valid_iter, model, device=gpu))
trainer.extend(chainer.training.extensions.dump_graph('main/loss'))
# Take a snapshot for each specified epoch
frequency = 10
trainer.extend(chainer.training.extensions.snapshot(filename="snapshot_cureent"), trigger=(frequency, 'epoch'))
trainer.extend(chainer.training.extensions.LogReport(trigger=(10, "epoch")))
trainer.extend(chainer.training.extensions.PrintReport(
["epoch", "main/loss", "validation/main/loss", "elapsed_time"]))
# trainer.extend(chainer.training.extensions.ProgressBar())
trainer.extend(chainer.training.extensions.PlotReport(['main/loss', 'validation/main/loss'], trigger=(10, "epoch"),
filename="loss.png"))
trainer.run()
# テストデータ
N_test = 50
test_ds,test_xval = get_dataset(N_test,3*np.pi,4*np.pi)
X_test,y_test,x=seq_split(seqlen,test_ds,test_xval)
with chainer.using_config("train", False), chainer.using_config('enable_backprop', False):
model_predict=[]
for xt in X_test:
model_predict.append(model.predict(np.array([xt],dtype=np.float32)))
y=F.concat(y_test,axis=0).data
p=F.concat(model_predict, axis=0).data
plt.plot(x,y,color="b")
plt.plot(x,p,color="r")
plt.show()
xが０から２πまでをN=100等分し、その時のyの値を学習します
出力
epoch main/loss validation/main/loss elapsed_time 10 0.412313 0.22419 0.680705 20 0.34348 0.176668 1.45632 30 0.322577 0.157206 2.21422 40 0.313264 0.142921 3.01513 50 0.286482 0.156473 3.79678 60 0.271693 0.145663 4.5567 70 0.26161 0.153716 5.27208 80 0.249188 0.148146 6.01087 90 0.229289 0.135516 6.7483 100 0.235577 0.135556 7.4885 110 0.210943 0.122771 8.23302 120 0.206481 0.125734 8.96983 130 0.199006 0.110476 9.70469 140 0.185752 0.105235 10.443 150 0.170962 0.0997412 11.2183 160 0.17236 0.0935808 11.9595 170 0.159314 0.08463 12.7018 180 0.159687 0.0768325 13.4395 190 0.137582 0.0830929 14.18 200 0.146723 0.0774658 14.9236 210 0.144295 0.0731078 15.6569 220 0.137017 0.0640324 16.3937 230 0.120282 0.0675966 17.1413 240 0.122946 0.065422 17.886 250 0.112485 0.0601812 18.6319 260 0.115785 0.0622176 19.3996 270 0.108337 0.0572397 20.1444 280 0.113232 0.0529092 20.8836 290 0.111058 0.0531542 21.6315 300 0.0978656 0.0537841 22.367 310 0.107318 0.0500048 23.1059 320 0.100115 0.0471024 23.8513 330 0.0941351 0.0466782 24.6336 340 0.0992865 0.0462204 25.4045 350 0.0909913 0.0444264 26.1611 360 0.0862495 0.04312 26.9144 370 0.0855708 0.0425527 27.7444 380 0.0872798 0.0402729 28.5102 390 0.0902846 0.0412268 29.265 400 0.0840953 0.0421445 30.0178 410 0.0782678 0.0389577 30.7646 420 0.0813485 0.0383136 31.5095 430 0.0892697 0.0380051 32.2756 440 0.0784913 0.0378043 33.0377 450 0.077315 0.0382185 33.7859 460 0.0797667 0.0370378 34.5328 470 0.085258 0.0353085 35.2766 480 0.0904794 0.0364417 36.0569 490 0.0760617 0.0347273 36.7939 500 0.0776822 0.0349566 37.5342 510 0.0753997 0.0348118 38.2753 520 0.084298 0.0351735 39.0137 530 0.0827682 0.0336927 39.7616 540 0.0885914 0.032941 40.4968 550 0.0755433 0.0328157 41.2496 560 0.0864087 0.0329004 41.9931 570 0.0696817 0.0333915 42.7455 580 0.0673041 0.0310085 43.4925 590 0.0695492 0.0322058 44.2814 600 0.0626493 0.0321012 45.0249 610 0.0780004 0.0311171 45.7709 620 0.0842924 0.0313559 46.5104 630 0.0869392 0.0310007 47.253 640 0.0807384 0.0300728 48.0017 650 0.061898 0.0308209 48.799 660 0.0656733 0.0304086 49.5613 670 0.0785108 0.0301482 50.3314 680 0.0748608 0.0305042 51.1063 690 0.0720685 0.0300295 51.874 700 0.071668 0.0300219 52.6741 710 0.0577448 0.0295377 53.4246 720 0.07059 0.0295795 54.1749 730 0.0677278 0.0291774 54.9278 740 0.0747214 0.0296802 55.6766 750 0.0796093 0.0296162 56.4188 760 0.0659514 0.0292572 57.1649 770 0.0651634 0.0294423 57.9178 780 0.0732363 0.0291244 58.6651 790 0.0750731 0.0292386 59.54 800 0.0768709 0.0289816 60.4078 810 0.0712155 0.0293295 61.1858 820 0.0613775 0.0290006 62.1138 830 0.0674119 0.0289881 62.9673 840 0.0720593 0.0289764 63.7099 850 0.0653162 0.028784 64.4681 860 0.0873163 0.0285498 65.2305 870 0.0674722 0.0286272 65.9901 880 0.0718548 0.0282714 66.7374 890 0.0659643 0.028604 67.5049 900 0.0790577 0.0286806 68.2621 910 0.0734288 0.028266 69.0192 920 0.0664547 0.0282677 69.7996 930 0.0799885 0.0284383 70.5581 940 0.0687402 0.0284575 71.3119 950 0.0721005 0.0282444 72.0637 960 0.0750532 0.0282908 72.8485 970 0.0663102 0.0282821 73.6094 980 0.0807248 0.0281474 74.3701 990 0.0730301 0.0283711 75.155 1000 0.0674249 0.0282971 75.9349
テスト結果
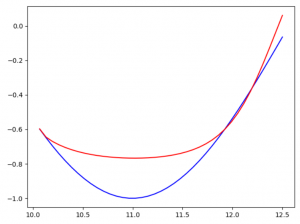
青い線が正解で赤い線が学習したのちの予測結果です。
Xの値を与えて、Yを予測した結果ですが、あまりうまく予測できていませんね